AVL Tree

AVL Tree ditemukan oleh Adelson-Velskii dan Landis. AVL Tree merupakan salah satu jenis BST (binary Search Tree). BST digunakan dengan tujuan untuk mempercepat pencarian data. Apabila BST yg terbentuk cukup seimbang (mendekati complete binary tree) maka waktu pencarian data tidak lebih dari log2n langkah.

AVL Tree adalah Binary Search Tree yang memiliki perbedaan tinggi/ level maksimal 1 antara subtree kiri dan subtree kanan. AVL Tree muncul untuk menyeimbangkan Binary Search Tree. Dengan AVL Tree, waktu pencarian dan bentuk tree dapat dipersingkat dan disederhanakan.

Insert

Ada 4 kasus yang biasanya terjadi saat operasi insert dilakukan, yaitu :
anggap T adalah node yang harus diseimbangkan kembali
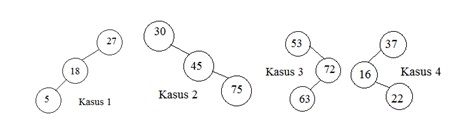
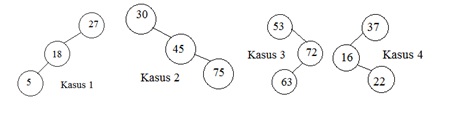
– Kasus 1 : node terdalam terletak pada subtree kiri dari anak kiri T (left-left)
– Kasus 2 : node terdalam terletak pada subtree kanan dari anak kanan T (right-right)
– Kasus 3 : node terdalam terletak pada subtree kanan dari anak kiri T (right-left)
– Kasus 4 : node terdalam terletak pada subtree kiri dari anak kanan T (left-right)

Ke-4 kasus tersebut dapat diselesaikan dengan melakukan rotasi
– Kasus 1 dan 2 dengan single rotation
– Kasus 3 dan 4 dengan double rotation

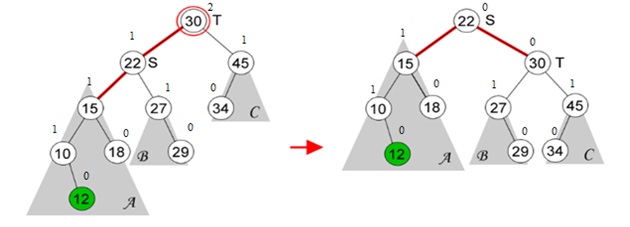
Contoh – Single Rotation: Jika suatu Tree diinsert node baru dengan nilai 12, maka akan terjadi ketidak seimbangan dan hal ini terletak pada posisi root

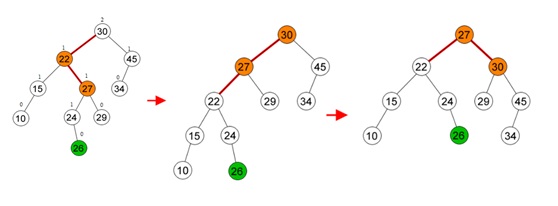
Contoh – Double Rotation : Jika terdapat sebuah tree yang kemudian dilakukan insert node 26. Maka akan terjadi ketidak seimbangan, sehingga terlihat dari bentuknya dapat diselesaikan dengan kasus 4.

AVL Tree adalah Binary Search Tree yang memiliki perbedaan tinggi/ level maksimal 1 antara subtree kiri dan subtree kanan. AVL Tree muncul untuk menyeimbangkan Binary Search Tree. Dengan AVL Tree, waktu pencarian dan bentuk tree dapat dipersingkat dan disederhanakan.

Delete

Ada 2 kasus yang biasanya terjadi saat operasi delete dilakukan, yaitu :
– Jika node yang akan dihapus berada pada posisi leaf atau node tanpa anak, maka dapat langsung di hapus.

• Jika node yang akan dihapus memiliki anak, maka proses penghapusannya harus di cek kembali untuk menyeimbangkan Binary Search Tree dengan perbedaan tinggi / level maksimal 1.
• anggap T adalah node yang harus diseimbangkan kembali
  – Kasus 1 : node terdalam terletak pada subtree kiri dari anak kiri T (left-left)
  – Kasus 2 : node terdalam terletak pada subtree kanan dari anak kanan T (right-right)
  – Kasus 3 : node terdalam terletak pada subtree kanan dari anak kiri T (right-left)
  – Kasus 4 : node terdalam terletak pada subtree kiri dari anak kanan T (left-right)
  

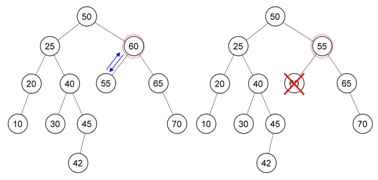
Berikut contoh dalam menghapus node AVL Tree, terdapat AVL Tree yang kemudian di hapus node 60. Dengan gambaran sebagai berikut :

Yang akan menggantikan posisi node 60 adalah node 55. Akan terjadi ketidak seimbangan. Dengan tampilan sebagai berikut :

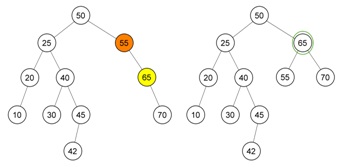
Maka akan dilakukan single rotation pada node 55 dengan kasus ketidak seimbangan pada kasus no. 2. Dengan tampilan setelah dilakukan single rotation sebagai berikut :

Ketika sudah dilakukan single rotation dan dilakukan kembali perbedaan tinggi / level maksimal 1 ternyata terdapat ketidak seimbangan yang terjadi. Sehingga diperlukan double rotation dengan kasus no. 4. Sehingga hasil dari rotasi yang dilakukan adalah sebagai berikut :